Draw a Circle Given Points

To draw a straight line, the minimum number of points required is two. That means we tin can describe a direct line with the given ii points. How many minimum points are sufficient to depict a unique circle? Is it possible to describe a circle passing through 3 points? In how many ways can nosotros draw a circle that passes through three points? Well, allow's try to discover answers to all these queries.

Learn: Circle Definition

Before drawing a circle passing through iii points, let's have a wait at the circles that have been fatigued through 1 and two points respectively.

Circle Passing Through a Point

Let us consider a indicate and try to draw a circle passing through that betoken.

Equally given in the figure, through a single indicate P, we tin can draw infinite circles passing through it.

Circle Passing Through Ii Points

Now, permit us have two points, P and Q and see what happens?

Again we see that an space number of circles passing through points P and Q can exist drawn.

Circumvolve Passing Through Three Points (Collinear or Not-Collinear)

Let us now take 3 points. For a circle passing through 3 points, two cases can arise.

• 3 points tin exist collinear
• Three points tin can be not-collinear

Let us written report both cases individually.

Instance 1: A circle passing through three points: Points are collinear

Consider iii points, P, Q and R, which are collinear.

If three points are collinear, any 1 of the points either prevarication outside the circle or inside it. Therefore, a circle passing through three points, where the points are collinear, is not possible.

Instance 2: A circumvolve passing through 3 points: Points are not-collinear

To draw a circle passing through three non-collinear points, we need to locate the centre of a circle passing through 3 points and its radius. Follow the steps given beneath to understand how we tin can draw a circle in this example.

Step i: Take three points P, Q, R and join the points equally shown below:

Footstep 2: Draw perpendicular bisectors of PQ and RQ. Let the bisectors AB and CD run across at O such that the point O is called the center of the circle.

Step 3: Describe a circle with O equally the centre and radius OP or OQ or OR. We get a circle passing through 3 points P, Q, and R.

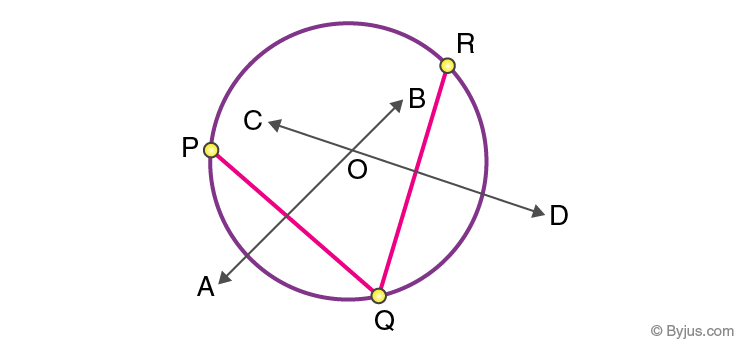
It is observed that just a unique circumvolve volition laissez passer through all three points. It can be stated as a theorem and the proof is explained as follows.

It is observed that only a unique circle will laissez passer through all iii points. It tin be stated as a theorem, and the proof of this is explained below.

Given:

Three non-collinear points P, Q and R

To prove:

Just one circle can be fatigued through P, Q and R

Construction:

Join PQ and QR.

Describe the perpendicular bisectors of PQ and QR such that these perpendiculars intersect each other at O.

Proof:

S. No	Statement	Reason
1	OP = OQ	Every point on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment.
2	OQ = OR	Every point on the perpendicular bisector of a line segment is equidistant from the endpoints of the line segment.
3	OP = OQ = OR	From (i) and (two)
4	O is equidistant from P, Q and R

If a circle is fatigued with O as eye and OP as radius, then it will also pass through Q and R.

O is the only point which is equidistant from P, Q and R as the perpendicular bisectors of PQ and QR intersect at O only.

Thus, O is the centre of the circle to be fatigued.

OP, OQ and OR will be radii of the circle.

From above information technology follows that a unique circle passing through 3 points can exist fatigued given that the points are non-collinear.

Till now, yous learned how to describe a circle passing through three non-collinear points. Now, yous will learn how to observe the equation of a circle passing through three points . For this we demand to take iii non-collinear points.

Circle Equation Passing Through three Points

Let's derive the equation of the circumvolve passing through the iii points formula.

Let P(ten₁, y₁), Q(x_two, y₂) and R(x₃, y_three) be the coordinates of three non-collinear points.

We know that,

The general form of equation of a circle is: ten² + y² + 2gx + 2fy + c = 0….(1)

Now, we need to substitute the given points P, Q and R in this equation and simplify to get the value of g, f and c.

Substituting P(x₁, y_ane) in equ(i),

x_i ² + y₁ ^two + 2gx₁ + 2fy_one + c = 0….(2)

10₂ ^two + y₂ ^two + 2gx_two + 2fy_two + c = 0….(iii)

x₃ ^two + y_three ² + 2gx₃ + 2fy₃ + c = 0….(four)

From (ii) we get,

2gx_ane = -x₁ ² – y_i ² – 2fy₁ – c….(five)

Again from (2) we get,

c = -ten_one ⁱⁱ – y₁ ^two – 2gx_one – 2fy₁….(6)

From (four) nosotros go,

2fy₃ = -x_iii ² – y₃ ² – 2gx_three – c….(seven)

Now, subtracting (three) from (2),

2g(x₁ – x_two) = (x_two ² -x₁ ²) + (y_ii ² – y₁ ^two) + 2f (y₂ – y₁)….(8)

Substituting (6) in (7),

2fy3 = -x₃ ² – y₃ ² – 2gx_three + x_one ⁱⁱ + y_ane ² + 2gx_i + 2fy₁….(9)

Now, substituting equ(viii), i.e. 2g in equ(ix),

2f = [(x₁ ^two – x₃ ²)(x_ane – 10_ii) + (y_one ² – y₃ ² )(x_ane – x_ii) + (ten₂ ² – x₁ ²)(x₁ – ten₃) + (y₂ ² – y₁ ²)(x_one – x₃)] / [(y_iii – y₁)(x_i – 10_two) – (y₂ – y_one)(10_ane – x₃)]

Similarly, nosotros can get 2g equally:

2g = [(ten_ane ² – x₃ ²)(y₁ – x₂) + (y_one ² – y₃ ²)(y₁ – y₂) + (x₂ ⁱⁱ – x₁ ²)(y_i – y₃) + (y_two ² – y_one ^two)(y₁ – y_iii)] / [(x₃ – x_i)(y_one – y_two) – (ten₂ – 10₁)(y₁ – y₃)]

Using these 2g and 2f values we can get the value of c.

Thus, past substituting g, f and c in (1) we volition get the equation of the circle passing through the given 3 points.

Solved Example

Question:

What is the equation of the circle passing through the points A(2, 0), B(-2, 0) and C(0, 2)?

Solution:

Consider the general equation of circle:

x² + y² + 2gx + 2fy + c = 0….(i)

Substituting A(2, 0) in (i),

(two)² + (0)² + 2g(2) + 2f(0) + c = 0

4 + 4g + c = 0….(2)

Substituting B(-2, 0) in (i),

(-2)² + (0)² + 2g(-2) + 2f(0) + c = 0

4 – 4g + c = 0….(iii)

Substituting C(0, 2) in (i),

(0)² + (2)^two + 2g(0) + 2f(2) + c = 0

four + 4f + c = 0….(iv)

Adding (ii) and (iii),

four + 4g + c + iv – 4g + c = 0

2c + viii = 0

2c = -8

c = -four

Substituting c = -4 in (two),

4 + 4g – four = 0

4g = 0

k = 0

Substituting c = -4 in (iv),

iv + 4f – 4 = 0

4f = 0

f = 0

At present, substituting the values of g, f and c in (i),

x^two + y² + 2(0)x + 2(0)y + (-4) = 0

xⁱⁱ + y² – 4 = 0

Or

x² + y² = iv

This is the equation of the circle passing through the given three points A, B and C.

To know more nigh the area of a circle, equation of a circle, and its properties download BYJU'S-The Learning App.

boydoudge1988.blogspot.com

Source: https://byjus.com/maths/circle-passing-through-3-points/

Share this post