At 1 Atm of Pressure and a Temperature of 0ã‚â°c, Which Phase(S) of H2o Can Exist?

Temperature and pressure point where phase boundaries disappear

1. Subcritical ethane, liquid and gas phase coexist.
2. Critical indicate (32.17 °C, 48.72 bar), opalescence.
3. Supercritical ethane, fluid.^[ane]

In thermodynamics, a critical point (or critical country) is the end point of a phase equilibrium curve. The most prominent example is the liquid–vapor critical bespeak, the end bespeak of the pressure–temperature curve that designates conditions under which a liquid and its vapor can coexist. At higher temperatures, the gas cannot exist liquefied past pressure alone. At the disquisitional indicate, defined by a disquisitional temperature T _c and a critical pressure p _c, stage boundaries vanish. Other examples include the liquid–liquid critical points in mixtures, and the ferromagnet-paramagnet transition in the absenteeism of an external magnetic field.^[2]

Liquid–vapor disquisitional betoken [edit]

Overview [edit]

The liquid–vapor critical point in a force per unit area–temperature stage diagram is at the loftier-temperature extreme of the liquid–gas phase purlieus. The dashed greenish line shows the dissonant beliefs of water.

For simplicity and clarity, the generic notion of disquisitional bespeak is best introduced past discussing a specific instance, the vapor-liquid critical point. This was the showtime disquisitional point to exist discovered, and information technology is nonetheless the best known and about studied one.

The effigy to the correct shows the schematic PT diagram of a pure substance (as opposed to mixtures, which have additional land variables and richer phase diagrams, discussed below). The commonly known phases solid, liquid and vapor are separated by stage boundaries, i.e. pressure–temperature combinations where two phases can coexist. At the triple indicate, all three phases can coexist. However, the liquid–vapor boundary terminates in an endpoint at some disquisitional temperature T _c and critical pressure p _c. This is the disquisitional point.

In h2o, the critical point occurs at 647.096 Yard (373.946 °C; 705.103 °F) and 22.064 megapascals (3,200.1 psi; 217.75 atm).^[3]

In the vicinity of the critical indicate, the physical properties of the liquid and the vapor change dramatically, with both phases becoming ever more similar. For instance, liquid water nether normal atmospheric condition is most incompressible, has a depression thermal expansion coefficient, has a loftier dielectric abiding, and is an fantabulous solvent for electrolytes. Most the critical signal, all these backdrop change into the exact opposite: water becomes compressible, expandable, a poor dielectric, a bad solvent for electrolytes, and prefers to mix with nonpolar gases and organic molecules.^[iv]

At the critical point, only one phase exists. The estrus of vaporization is zero. There is a stationary inflection point in the constant-temperature line (disquisitional isotherm) on a PV diagram. This means that at the critical point:^{[5] [six] [seven]}

${\displaystyle \left({\frac {\partial p}{\partial V}}\right)_{T}=0,}$

${\displaystyle \left({\frac {\partial ^{2}p}{\partial 5^{2}}}\right)_{T}=0.}$

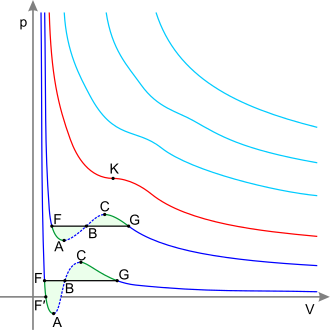
The disquisitional isotherm with the critical point G

To a higher place the critical point in that location exists a state of matter that is continuously connected with (tin can be transformed without stage transition into) both the liquid and the gaseous land. It is called supercritical fluid. The mutual textbook knowledge that all stardom between liquid and vapor disappears beyond the critical indicate has been challenged past Fisher and Widom,^[8] who identified a p–T line that separates states with dissimilar asymptotic statistical properties (Fisher–Widom line).

Sometimes^{[ ambiguous ]} the critical indicate does not manifest in most thermodynamic or mechanical properties, only is "subconscious" and reveals itself in the onset of inhomogeneities in elastic moduli, marked changes in the appearance and local properties of not-affine droplets, and a sudden enhancement in defect pair concentration.^[9]

History [edit]

Critical carbon dioxide exuding fog while cooling from supercritical to critical temperature.

The existence of a critical point was first discovered past Charles Cagniard de la Tour in 1822^{[10] [11]} and named by Dmitri Mendeleev in 1860^{[12] [13]} and Thomas Andrews in 1869.^[14] Cagniard showed that CO₂ could be liquefied at 31 °C at a pressure level of 73 atm, but non at a slightly higher temperature, fifty-fifty under pressures equally high equally 3000 atm.

Theory [edit]

Solving the to a higher place status ${\displaystyle (\partial p/\partial V)_{T}=0}$ for the van der Waals equation, 1 tin can compute the critical indicate as

${\displaystyle T_{\text{c}}={\frac {8a}{27Rb}},\quad V_{\text{c}}=3nb,\quad p_{\text{c}}={\frac {a}{27b^{2}}}.}$

Withal, the van der Waals equation, based on a mean-field theory, does non hold near the disquisitional bespeak. In particular, it predicts wrong scaling laws.

To analyse properties of fluids about the critical point, reduced country variables are sometimes defined relative to the critical properties^[15]

${\displaystyle T_{\text{r}}={\frac {T}{T_{\text{c}}}},\quad p_{\text{r}}={\frac {p}{p_{\text{c}}}},\quad V_{\text{r}}={\frac {V}{RT_{\text{c}}/p_{\text{c}}}}.}$

The principle of corresponding states indicates that substances at equal reduced pressures and temperatures have equal reduced volumes. This relationship is approximately true for many substances, but becomes increasingly inaccurate for large values of p _r.

For some gases, there is an boosted correction factor, called Newton'southward correction, added to the critical temperature and disquisitional force per unit area calculated in this manner. These are empirically derived values and vary with the pressure range of interest.^[16]

Table of liquid–vapor critical temperature and force per unit area for selected substances [edit]

Substance[17] [18]	Critical temperature	Disquisitional pressure (accented)
Argon	−122.4 °C (150.eight K)	48.1 atm (four,870 kPa)
Ammonia (NH3)[nineteen]	132.4 °C (405.5 K)	111.3 atm (11,280 kPa)
R-134a	101.06 °C (374.21 K)	40.06 atm (4,059 kPa)
R-410A	72.viii °C (345.nine Thou)	47.08 atm (iv,770 kPa)
Bromine	310.8 °C (584.0 Grand)	102 atm (10,300 kPa)
Caesium	ane,664.85 °C (i,938.00 K)	94 atm (9,500 kPa)
Chlorine	143.8 °C (416.9 K)	76.0 atm (7,700 kPa)
Ethanol (C2H5OH)	241 °C (514 Chiliad)	62.18 atm (6,300 kPa)
Fluorine	−128.85 °C (144.30 K)	51.v atm (v,220 kPa)
Helium	−267.96 °C (5.19 One thousand)	2.24 atm (227 kPa)
Hydrogen	−239.95 °C (33.20 M)	12.8 atm (1,300 kPa)
Krypton	−63.eight °C (209.three Grand)	54.3 atm (five,500 kPa)
Methane (CHiv)	−82.three °C (190.8 K)	45.79 atm (four,640 kPa)
Neon	−228.75 °C (44.40 Thousand)	27.2 atm (2,760 kPa)
Nitrogen	−146.ix °C (126.2 K)	33.5 atm (3,390 kPa)
Oxygen (O2)	−118.half dozen °C (154.half dozen K)	49.viii atm (5,050 kPa)
Carbon dioxide (CO2)	31.04 °C (304.19 K)	72.viii atm (vii,380 kPa)
Nitrous oxide (N2O)	36.iv °C (309.5 K)	71.5 atm (7,240 kPa)
Sulfuric acid (H2SO4)	654 °C (927 K)	45.iv atm (4,600 kPa)
Xenon	16.vi °C (289.eight K)	57.six atm (v,840 kPa)
Lithium	2,950 °C (3,220 Thou)	652 atm (66,100 kPa)
Mercury	1,476.nine °C (1,750.1 K)	i,720 atm (174,000 kPa)
Sulfur	1,040.85 °C (1,314.00 K)	207 atm (21,000 kPa)
Iron	8,227 °C (viii,500 K)
Gilded	6,977 °C (7,250 Thou)	5,000 atm (510,000 kPa)
Aluminium	7,577 °C (7,850 K)
Water (HiiO)[iii] [xx]	373.946 °C (647.096 K)	217.seven atm (22,060 kPa)

Mixtures: liquid–liquid critical indicate [edit]

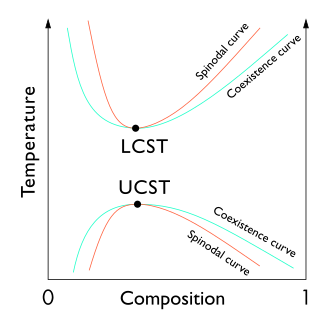
A plot of typical polymer solution phase behavior including two critical points: a LCST and an UCST

The liquid–liquid disquisitional betoken of a solution, which occurs at the critical solution temperature, occurs at the limit of the ii-stage region of the phase diagram. In other words, it is the indicate at which an infinitesimal alter in some thermodynamic variable (such as temperature or pressure) leads to separation of the mixture into two singled-out liquid phases, as shown in the polymer–solvent phase diagram to the right. Two types of liquid–liquid critical points are the upper critical solution temperature (UCST), which is the hottest point at which cooling induces phase separation, and the lower critical solution temperature (LCST), which is the coldest bespeak at which heating induces phase separation.

Mathematical definition [edit]

From a theoretical standpoint, the liquid–liquid disquisitional signal represents the temperature–concentration extremum of the spinodal curve (as can be seen in the figure to the right). Thus, the liquid–liquid critical point in a two-component system must satisfy two weather condition: the condition of the spinodal curve (the 2d derivative of the costless energy with respect to concentration must equal zero), and the extremum status (the tertiary derivative of the costless energy with respect to concentration must also equal nil or the derivative of the spinodal temperature with respect to concentration must equal zero).

See too [edit]

• Conformal field theory
• Disquisitional exponents
• Disquisitional phenomena (more advanced article)
• Critical points of the elements (information folio)
• Curie betoken
• Joback method, Klincewicz method, Lydersen method (interpretation of disquisitional temperature, pressure, and volume from molecular structure)
• Liquid–liquid critical point
• Lower critical solution temperature
• Néel bespeak
• Percolation thresholds
• Stage transition
• Rushbrooke inequality
• Scale invariance
• Self-organized criticality
• Supercritical fluid, Supercritical drying, Supercritical water oxidation, Supercritical fluid extraction
• Tricritical point
• Triple point
• Upper critical solution temperature
• Widom scaling

Footnotes [edit]

1. ^ Horstmann, Sven (2000). Theoretische und experimentelle Untersuchungen zum Hochdruckphasengleichgewichtsverhalten fluider Stoffgemische für die Erweiterung der PSRK-Gruppenbeitragszustandsgleichung [Theoretical and experimental investigations of the loftier-pressure phase equilibrium behavior of fluid mixtures for the expansion of the PSRK group contribution equation of state] (Ph.D.) (in German). Oldenburg, Germany: Carl-von-Ossietzky Universität Oldenburg. ISBN3-8265-7829-5. OCLC 76176158.
2. ^ Stanley, H. Eugene (1987). Introduction to phase transitions and critical phenomena. New York: Oxford University Press. ISBN0-nineteen-505316-8. OCLC 15696711.
3. ^ ^{a b} Wagner, W.; Pruß, A. (June 2002). "The IAPWS Formulation 1995 for the Thermodynamic Backdrop of Ordinary Water Substance for General and Scientific Use". Journal of Physical and Chemical Reference Data. 31 (two): 398. doi:x.1063/1.1461829.
4. ^ Anisimov, Sengers, Levelt Sengers (2004): About-critical behavior of aqueous systems. Chapter ii in Aqueous System at Elevated Temperatures and Pressures Palmer et al., eds. Elsevier.
5. ^ P. Atkins and J. de Paula, Physical Chemistry, 8th ed. (Due west. H. Freeman 2006), p. 21.
6. ^ 1000. J. Laidler and J. H. Meiser, Physical Chemistry (Benjamin/Cummings 1982), p. 27.
7. ^ P. A. Rock, Chemic Thermodynamics (MacMillan 1969), p. 123.
8. ^ Fisher, Widom: Decay of Correlations in Linear Systems, J. Chem. Phys. 50, 3756 (1969).
9. ^ Das, Tamoghna; Ganguly, Saswati; Sengupta, Surajit; Rao, Madan (3 June 2015). "Pre-Yield Non-Affine Fluctuations and A Hidden Critical Point in Strained Crystals". Scientific Reports. v (1): 10644. Bibcode:2015NatSR...510644D. doi:10.1038/srep10644. PMC4454149. PMID 26039380.
10. ^ Charles Cagniard de la Tour (1822). "Exposé de quelques résultats obtenu par l'action combinée de la chaleur et de la compression sur certains liquides, tels que 50'eau, l'alcool, l'éther sulfurique et l'essence de pétrole rectifiée" [Presentation of some results obtained by the combined activeness of estrus and compression on certain liquids, such equally h2o, alcohol, sulfuric ether (i.e., diethyl ether), and distilled petroleum spirit]. Annales de Chimie et de Physique (in French). 21: 127–132.
11. ^ Berche, B., Henkel, Grand., Kenna, R (2009) Critical phenomena: 150 years since Cagniard de la Bout. Periodical of Physical Studies 13 (3), pp. 3001-1–3001-iv.
12. ^ Mendeleev called the critical point the "accented temperature of humid" (Russian: абсолютная температура кипения; German: absolute Siedetemperatur).
    • Менделеев, Д. (1861). "О расширении жидкостей от нагревания выше температуры кипения" [On the expansion of liquids from heating above the temperature of humid]. Горный Журнал [Mining Journal] (in Russian). 4: 141–152. The "absolute temperature of boiling" is defined on p. 151. Available at Wikimedia
    • German translation: Mendelejeff, D. (1861). "Ueber die Ausdehnung der Flüssigkeiten beim Erwärmen über ihren Siedepunkt" [On the expansion of fluids during heating to a higher place their boiling signal]. Annalen der Chemie und Pharmacie (in German). 119: one–11. doi:x.1002/jlac.18611190102. The "absolute temperature of humid" is divers on p. 11: " Als absolute Siedetemperatur müssen wir den Punkt betrachten, bei welchem one) die Cohäsion der Flüssigkeit = 0° ist und a² = 0, bei welcher 2) dice latente Verdamfungswärme auch = 0 ist und bei welcher sich 3) die Flüssigkeit in Dampf verwandelt, unabhängig von Druck und Volum." (As the "accented temperature of humid" we must regard the point at which (1) the cohesion of the liquid equals 0° and a ² = 0 [where a ² is the coefficient of capillarity, p. 6], at which (2) the latent heat of vaporization also equals nix, and at which (3) the liquid is transformed into vapor, independently of the force per unit area and the volume.)
    • In 1870, Mendeleev asserted, confronting Thomas Andrews, his priority regarding the definition of the critical signal: Mendelejeff, D. (1870). "Bemerkungen zu den Untersuchungen von Andrews über dice Compressibilität der Kohlensäure" [Comments on Andrews' investigations into the compressibility of carbon dioxide]. Annalen der Physik. 2nd series (in High german). 141: 618–626. doi:10.1002/andp.18702171218.
13. ^ Landau, Lifshitz, Theoretical Physics, Vol. V: Statistical Physics, Ch. 83 [German edition 1984].
14. ^ Andrews, Thomas (1869). "The Bakerian lecture: On the continuity of the gaseous and liquid states of matter". Philosophical Transactions of the Royal Gild. London. 159: 575–590. doi:10.1098/rstl.1869.0021. The term "critical point" appears on page 588.
15. ^ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an applied science approach. Boston: McGraw-Colina. pp. 91–93. ISBN978-0-07-121688-three.
16. ^ Maslan, Frank D.; Littman, Theodore M. (1953). "Compressibility Chart for Hydrogen and Inert Gases". Ind. Eng. Chem. 45 (7): 1566–1568. doi:x.1021/ie50523a054.
17. ^ Emsley, John (1991). The Elements (Second ed.). Oxford University Press. ISBN978-0-nineteen-855818-7.
18. ^ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: An Engineering Approach (Fourth ed.). McGraw-Loma. pp. 824. ISBN978-0-07-238332-iv.
19. ^ "Ammonia - NH3 - Thermodynamic Properties". www.engineeringtoolbox.com . Retrieved 2017-04-07 .
20. ^ "Critical Temperature and Pressure". Purdue University. Retrieved 2006-12-19 .

References [edit]

• "Revised Release on the IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of H2o and Steam" (PDF). International Clan for the Properties of Water and Steam. Baronial 2007. Retrieved 2009-06-09 .

External links [edit]

• "Disquisitional points for some mutual solvents". ProSciTech. Archived from the original on 2008-01-31.
• "Critical Temperature and Pressure level". Department of Chemistry. Purdue University. Retrieved 2006-12-03 .

boydoudge1988.blogspot.com

Source: https://en.wikipedia.org/wiki/Critical_point_(thermodynamics)

Share this post